Phase Singularities In Resonant Metasurfaces
Remi Colom1, Elena Mikheeva1, Patrice Genevet3
1Université Côte d’Azur, CNRS, CRHEA, 06560 Valbonne, France
2Physics department, Colorado School of Mines, 1523 Illinois St., Golden, CO-80401, USA
Optical metasurfaces have recently emerged as an active field of research. They possess many advantages compared to conventional refractive optical components such as being ultra-thin and allowing to realize components with unconventional optical functionalities. Design of metasurfaces requires to have a careful control over the amplitude and phase of the reflected and/or transmitted fields. Components with large or even unitary transmission or reflection coefficients while being able to span the full [0,2π] phase range are particularly valuable. It is consequently valuable to identify the mechanisms influencing the amplitude and phase of metasurfaces. Here, we propose to study the response of metasurfaces for complex-frequency excitations to improve the understanding of the optical response of metasurface. In particular, we show that the relative positions of two types of phase singularities : zeros and poles of the transmission or reflection coefficients in the complex frequency plane allow to clearly predict when thereflection or transmission is unitary and when the phase spans the full [0,2π] interval. We also provide a link between the position of zeros in the complex plane and the symmetries of the metasurface to facilitate the design and realization of optical metasurfaces.
We will illustrate the usefulness of this approach by designing a metasurface in reflection with unitary amplitude and the phase covering the range [0,2π]. This behavior may be obtained when a reflection zero and pole are complex-conjugated. Symmetry considerations suggest that this behavior may be obtained by a metasurface breaking the top/down symmetry. Here, we consider an array of silicon (nSi = 3.5) nanocones (height=600 nm, period= 800nm and varying top and bottom diameters) illuminated from the top embedded in an homogeneous medium of refractive index 1.5 shown in Fig.1. We break the top/down symmetry by varying the top diameter compared to the bottom one. Results of simulations of the reflection coefficient computed finite element method are shown in Fig. 1 for a metasurface with a bottom diameter 500 nm and a top diameter equal to 420 nm for both real frequencies (lower left figure) and maps in the complex plane right top (logarithm of the amplitude) and bottom (phase). We observe a zero and a pole which are complex conjugated. Simulations at real frequencies confirm that the reflection amplitude is almost unitary and a phase that varies between 0 and 2π.
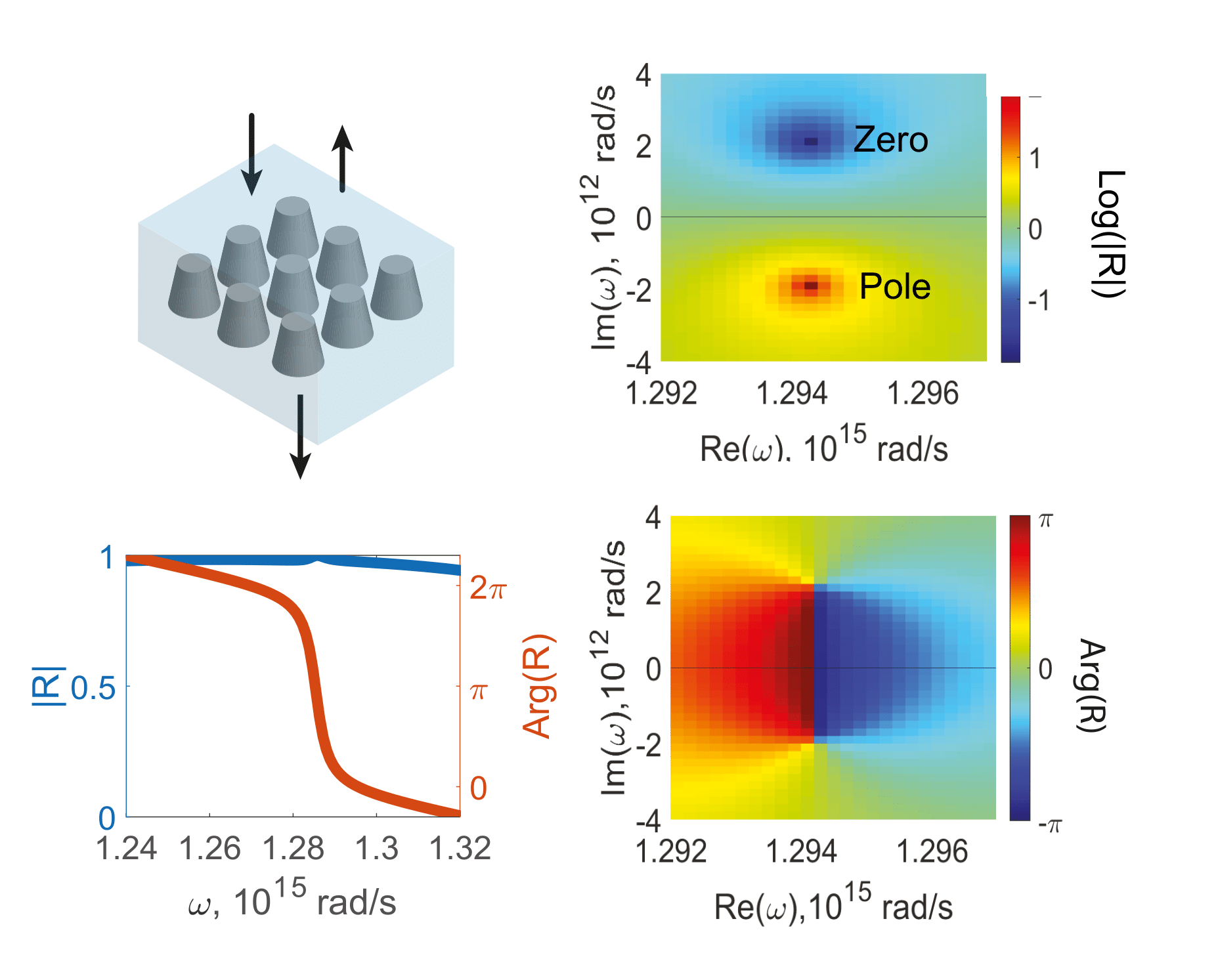
Silicon nanocone metasurface. Amplitude and phase of the reflection coefficient for real frequencies (bottom left). Maps of log(|R|) (top right) and Arg(R) bottom in the complex frequency plane.

